Table of Contents
Mean-
Question- Calculating the means from the following frequency distribution by Long Method-
| Class Interval C.I. | Frequency f |
| 40-44 | 3 |
| 35- 39 | 4 |
| 30 -34 | 5 |
| 25-29 | 6 |
| 20- 24 | 6 |
| 15-19 | 3 |
| 10-14 | 2 |
| 5- 9 | 1 |
| N= 30 |
दीर्घ विधि से मध्यमान ज्ञात करनें की विधि–
- वर्गान्तरों का मध्य बिन्दु ज्ञात कीजिए।
- मध्य बिन्दु का गुणा आवृत्ति से करके FX उनका गुणनफल ज्ञात कर लीजिए।
- तत्पश्चात FX का योग Sigma FX ज्ञात कर लिजिए।
- तत्पश्चात सिग्मा fx को N से भाग देकर मध्यमान ज्ञात कर लीजिये।
प्रयुक्त सूत्र-

Solution-
| Class Interval CI | Frequency f | X | fx |
| 40 – 44 | 3 | 42 | 126 |
| 35 – 39 | 4 | 37 | 148 |
| 30 – 34 | 5 | 32 | 160 |
| 25 – 29 | 6 | 27 | 162 |
| 20 – 24 | 6 | 22 | 132 |
| 15 – 19 | 3 | 17 | 51 |
| 10 – 14 | 2 | 12 | 24 |
| 5 – 9 | 1 | 7 | 7 |
| N = 30 | Σ fx = 810 | ||
Mean = Σfx / N
= 810 / 30
= 27 (Answer).
Median मध्यांक –
प्रश्न– निम्न लिखित आवृत्ति वितरण से मध्यांक की गणना कीजीए।
Calculate the median from the following frequency distribution.
| वर्गान्तर C.I.
Class Interval |
Frequency f
आवृत्ति |
| 40-44 | 7 |
| 35-39 | 9 |
| 30-34 | 12 |
| 25-29 | 15 |
| 20-24 | 7 |
| 15-19 | 9 |
| 10-14 | 1 |
| योग N – 60 |
Rules to Find the Median-
- संचयी आवृत्तियों को ज्ञात कर लिजिए।
- N/2 ज्ञात कर लीजिए।
- संचयी आवृत्ति वाले स्तम्भ से ज्ञात कर लीजिये कि N/2 के बराबर आवृत्तियां किस वर्गान्तर में हैं।इसे मध्यांक वर्गान्तर भी कहते हैं।
- जिस वर्गान्तर में मध्यांक पड़ता है उसकी निम्नतम सीमा ज्ञात कर लीजिए।
- जिस वर्गांतर में मध्यांक पड़ रहा है, उसकी आवृत्ति ज्ञात कर लीजिये।
- जिस वर्गान्तर में मध्यांक पड़ा है उसेक नीचे वाली वर्गान्तर की संचयी आवृत्ति ज्ञा त कर लीजिए।
- वर्ग विस्तार ज्ञात कर लिजीए।
- फिर निम्न सूत्र का प्रयोग किया जाता है।
सूत्र-
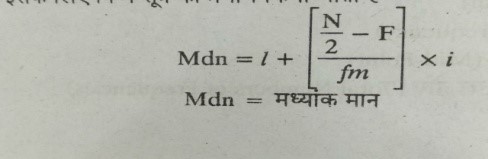
L= मध्यांक वर्गान्तर की वास्तविक निम्नतम सीमा
N/2 = कुल आवृत्तियों का आधा
F= मध्यांक वर्गान्तर के नीचे के वर्गान्तर की संचयी बारम्बारता
Fm= मध्यांक वर्गान्तर की आवृत्ति
I= वर्गान्तर का आकार
हल–
| वर्गान्तर
Class interval |
आवृत्ति
Frequency f |
संचयी आवृत्ति
|
| 40-44 | 7 | 60 |
| 35 – 39 | 9 | 53 |
| 30 – 34 | 12 fm | 44- मध्यांक वर्गान्तर |
| 25 – 29 | 15 | 32 F |
| 20 – 24 | 7 | 17 |
| 15 – 19 | 9 | 10 |
| 10- 14 | 1 | 1 |
| N = 60 |
Here N/2 = 60/2 = 30
L = 29.5
F = 32
Fm= 12
I= 5
Put these value in formula=
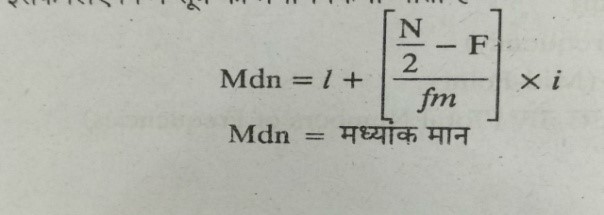
We get-
29.5 + {( 30- 32)/ 12} X 5
= 29.5 – (2/12) X 5
= 176/6
= 28.66
Answer.
बहुलांक Mode–
सूत्र–
M = 3 Median – 2 Mean
अर्थात पहले मध्यमान और मध्यांक ज्ञात करके उसके वैल्यू को उपर्युक्त सूत्र में प्रतिस्थापित करके हम बहुलांक ज्ञात कर लेते हैं।
आपको ये पोस्ट कैसी लगी, हमें आपकी प्रतिक्रिया Feedback का इंतजार रहेगा। नीचे कमेंट अवश्य करें।